 อ่านบทความนี้ใน Facebook
อ่านบทความนี้ใน Facebook
“การ breakdown ปัญหาใหญ่ให้เป็นปัญหาย่อย ๆ ที่ทับซ้อนกัน จากนั้นใช้การจำเพื่อลดการคำนวนที่ซ้ำซ้อน เพื่อให้แก้ปัญหาได้ไวขึ้น”
ข้อความข้างต้นเป็นนิยามคร่าว ๆ ที่เราได้คุยกันไปในบทความ “dynamic programming คืออะไร? เข้าใจใน 1 นาที”
สำหรับในบทความนี้ เราอยากมาชวนทำให้ภาพของประโยคดังกล่าวชัดขึ้น ผ่าน structure ที่เรารู้จักกันเป็นอย่างดีอย่าง tree (rooted tree) และ graph
ก่อนอื่นถ้าหากว่าเรามาดูตัวอย่างปัญหาสุด classic อย่าง fibonacci ที่มี recursive definition ว่า
- recursive case: \(f(n) = f(n-1) + f(n-2)\)
- base case: \(f(1) = 1; f(0) = 0\)
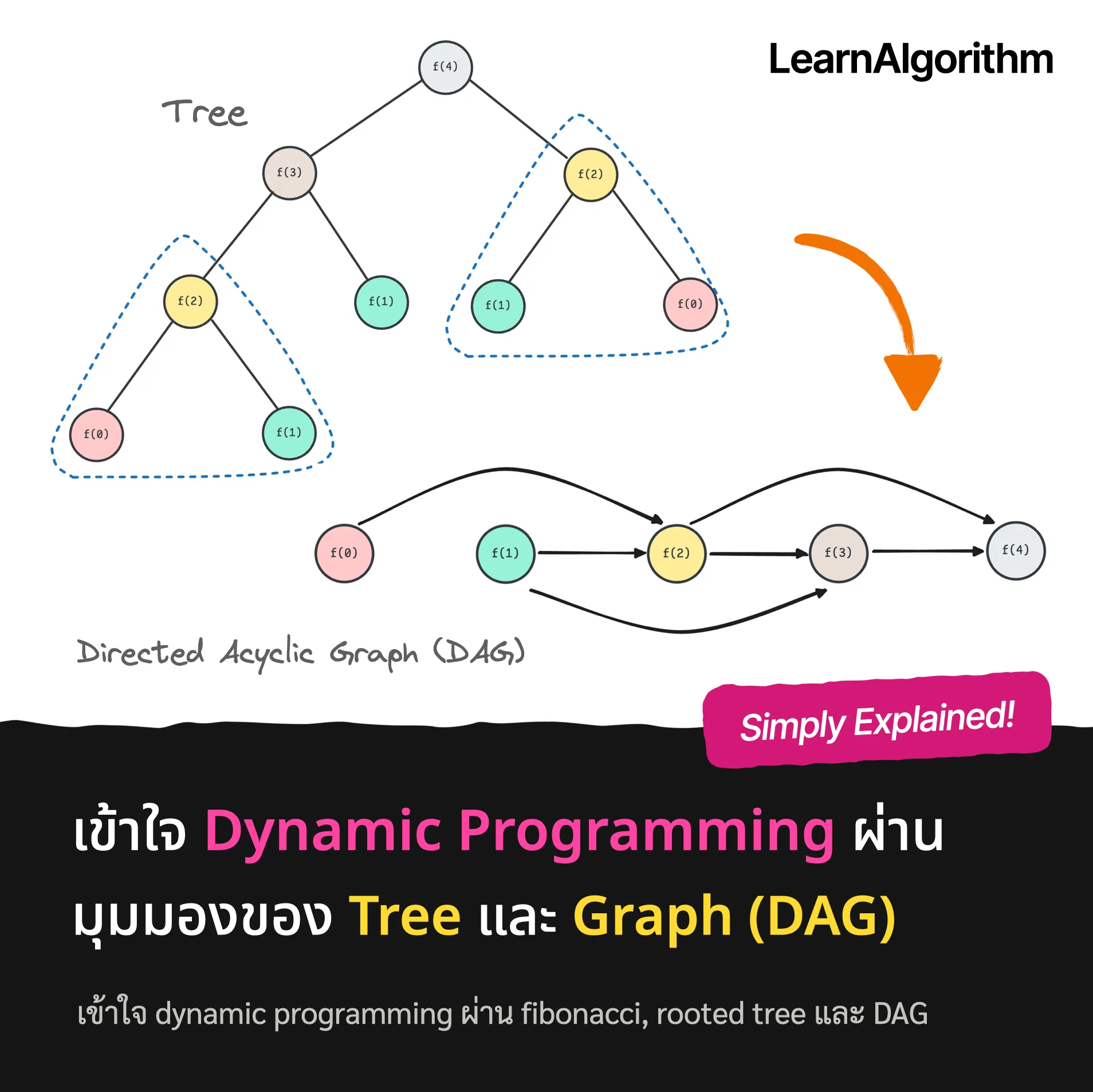
ถ้าหากว่าเราเราเรียก \(f(4)\) เราจะพบว่า การจะคำนวน \(f(4)\) ได้นั้นจะต้องคำนวน \(f(3)\), \(f(2)\) ก่อน และการจะคำนวน \(f(3)\) เราจะต้องคำนวน \(f(2)\), \(f(1)\) ไปเรื่อย ๆ … ซึ่งสุดท้ายแล้วเราจะสามารถวาดภาพ process ดังกล่าวออกมาเป็น tree (แบบภาพแรก) นั่นเอง
อย่างไรก็ตามจะเห็นว่า tree ดังกล่าวมันมีการคำนวนที่ซ้ำซ้อนกันมาก (สีเดียวกันคือปัญหาเดียวกัน และจะเห็นว่าเราต้องคำนวนสีเหลืองตั้ง 3 ที!!)
ดังนั้นจะเกิดอะไรขึ้นถ้าหากว่าเราลากลูกศรใหม่ โดยให้ไม่มีสีซ้ำกัน!?
ภาพที่เกิดขึ้นก็คือภาพที่สองนั่นเองครับ จะเห็นว่าคราวนี้ไม่มีการคำนวนที่ทับซ้อนกันอีกแล้ว; จากเดิมที่เราต้องคำนวนถึง \(O(2^n)\) ตอนนี้เหลือเพียง \(O(n)\) เท่านั้น
ซึ่งสำหรับการคำนวนเพื่อหาคำตอบสุดท้ายนั้น เราก็แค่คำนวนเริ่มจาก vertex ที่ไม่มีลูกศรชี้เข้า จากนั้นก็คำนวนตามลูกศรไปเรื่อย ๆ จนกระทั่งถึง vertex สุดท้าย
เราเรียก graph ดังกล่าวว่า directed acyclic graph หรือ DAG นั่นเองครับ; directed = มีลูกศร มีทิศทาง ส่วน acyclic คือไม่มี cycle ใน graph
สุดท้ายนี้จะเห็นว่า จริง ๆ แล้ว dynamic programming ในอีกมุมนั่นก็คือ “การลดรูปจาก tree ให้กลายเป็น DAG เพื่อลดการคำนวนที่ทับซ้อนลง” นั่นเอง
