 อ่านบทความนี้ใน Facebook
อ่านบทความนี้ใน Facebook
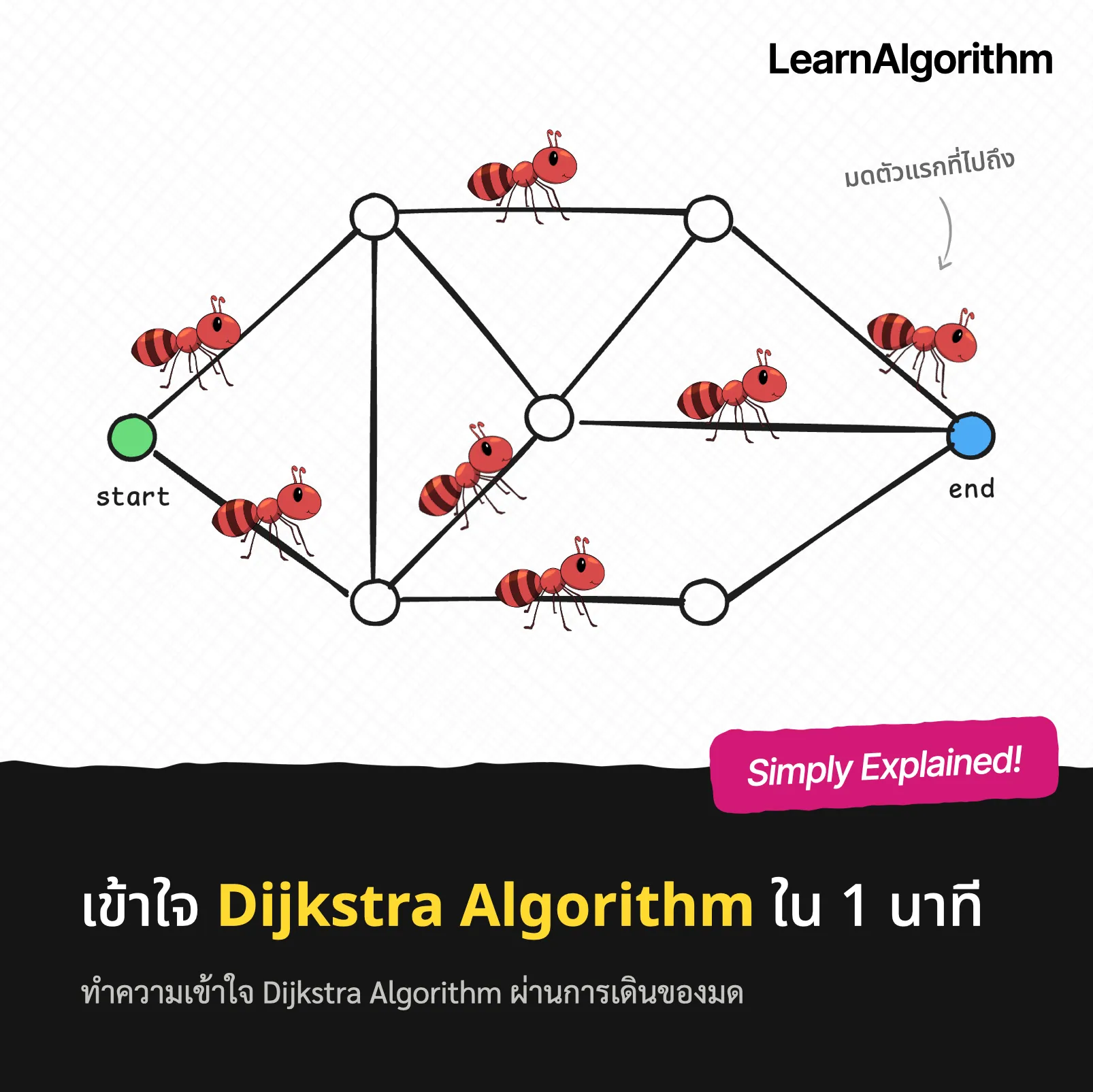
“มดตัวแรก 🐜 ที่เดินไปถึง end node เป็นมดที่เดินในเส้นทางที่เป็น shortest path จาก start node หรือไม่?”
ลองคิดภาพว่าเราปล่อยมดจำนวนมาก ๆ ไปที่จุด start node ของ graph (มดแต่ละตัวใช้ความเร็วในการเดินเท่ากัน) มดก็เดินกระจาย ๆ กันออกไปในเส้นทางต่าง ๆ ที่ติดกัน
และเมื่อปล่อยไปซักพัก แน่นอนว่าจะต้องมีมดสักตัวเดินไปถึง end node; คำถามคือเส้นทางเดินของมดตัวนั้นคือ shortest path หรือไม่?
คำตอบก็คือ “ใช่ครับ!” ถ้ามดทุกตัวเดินด้วยความเร็วที่เท่ากัน ดังนั้นการที่มดตัวหนึ่งไปถึงจุดใดจุดหนึ่งได้ก่อนมดตัวอื่น ก็หมายความว่า …มดตัวนั้น “เดินในระยะทางที่สั้นกว่า” นั่นเอง
ไอเดียข้างต้นเป็นไอเดียหลักของ Dijkstra’s algorithm ที่เป็น shortest path algorithm ที่นิยมมาก ๆ ตัวหนึ่งครับ
ซึ่งโดยหลักการแล้วก็คือจำลองการกระจายมด (visit node ตามลำดับที่มดตัวแรกเดินไปถึง) จากนั้นพอมดเดินไปถึง end node แล้ว ก็คำนวนเส้นทางย้อนกลับ เพื่อหาว่าจาก start ไป end นั้นเดินผ่านเส้นทางไหนบ้าง
ความน่าสนใจก็คือ ถ้าเราลองนึกถึงตัวอย่างข้างต้นดี ๆ เราก็จะพบว่า ไม่ใช่กับแค่ end node เท่านั้น
“แต่มดตัวแรกที่เดินไปถึงจุดใด ๆ ก็ตาม” เส้นทางของมดตัวนั้นก็คือ “shortest path ระหว่าง start node ไปถึงจุด ๆ นั้นทั้งสิ้น”
นั่นหมายความว่า Dijkstra’s algorithm ไม่ได้ใช้แค่การหา shortest path ระหว่างจุดสองจุดเท่านั้น แต่ใช้ในการหา “shortest path ของ start node กับทุก ๆ node ใน graph”
เราเรียกว่า SSSP หรือย่อมาจาก single-source shortest path algorithm
ส่วนตัวเราชอบคำอธิบายข้างต้นมาก แล้วก็ใช้เป็นตัวอย่างหลักเวลาอธิบาย dijkstra algorithm มาตลอด หวังว่าพออ่านแล้วทุกคนจะเห็นภาพ algorithm นี้มากขึ้น ไม่มากก็น้อยนะครับ
