เราไม่ชอบคณิตศาสตร์เพราะเรากำลังเข้าใจมันผิดอยู่รึป่าว?

ในบทความนี้เราอยากจะมาเล่ามุมมองต่อวิชาคณิตศาสตร์ของตัวเราเอง และอยากจะชวนทุกคนมานั่งคุยกันว่า คณิตศาสตร์ ในความเข้าใจของแต่ละคนคืออะไร มีหน้าตาเป็นยังไง จากคนที่เคยไม่ชอบและเรียนวิชาคณิตศาสตร์แบบไม่ได้เข้าใจมันมาก่อน

ดังนั้นก่อนที่จะเริ่ม เราอยากจะเล่าถึง background ของตัวเองสักนิดนึง

ย้อนกลับไปช่วงมัธยม

ย้อนกลับไปช่วง ม.6 เราเองก็เป็นนักเรียนคนนึงที่ไม่ค่อยได้สนใจการเรียนอะไรเท่าไหร่ ถ้าถามว่าตอนนั้นชอบวิชาคณิตศาสตร์ไหมก็คงจะตอบว่า ไม่ได้ชอบ แล้วก็ไม่ได้เกลียด ที่ไม่ได้ชอบเพราะรู้สึกไม่ได้เห็นความสำคัญขนาดนั้น แล้วก็ไม่ได้เกลียดเพราะเป็นวิชาที่ทำได้ดี (ส่วนหนึ่งอาจจะเพราะมันจำน้อย + มีความเป็น puzzle) เมื่อเทียบกับวิชาอื่น ๆ เช่น เคมี ชีวะ อะไรพวกนั้น

แต่อันที่เกลียดสุด ๆ ก็มีเหมือนกันเช่น การคำนวณพวกสูตรตรีโกณอะไรพวกนี้ เพราะสูตรโคตรเยอะ ต้องนั่งท่องนั่งจำ แถมตอนนั้นเราก็ไม่เคยได้มาตั้งคำถามเลยว่าสูตรพวกนี้มันเอาไปใช้ทำอะไร แล้วทำไมหน้าตามันถึงเป็นอย่างนั้น

พอเข้ามหาลัยมาก็มาเจอวิชา Calculus ซึ่งก็สูตรเยอะเหมือนเดิม เรียนแล้วหลับเหมือนเดิม สุดท้ายเลยต้องมาพยายามทำความเข้าใจอะไรหลาย ๆ อย่างเอง แต่รอบนี้เราลองเปิดใจมากขึ้น ลองพยายามเข้าใจเหตุและผลเบื้องหลังมากขึ้น เช่น ทำไม diff แล้วถึงได้ความชัน แล้วสูตร diff ที่ท่อง ๆ กันนี่มันมาจากไหน ถึงได้รู้ว่า อ๋อ จริง ๆ แล้วมันก็คือการวาดจุดบนกราฟ แบบติดกันมาก ๆ สองจุด แล้วลากเส้นเชื่อมสองจุดเป็นเส้นตรง และหาความชันจากเส้นตรงนั้น

พอได้เริ่มทำความเข้าใจแนวคิดความเป็นมาที่อยู่เบื้องหลังสูตรต่าง ๆ แล้ว มันทำให้เรารู้สึกว่า จริง ๆ แล้ว สูตรและสมการที่ดูน่ากลัวเหล่านั้น มันซ่อนความหมาย ภาพ หรือความคิดบางอย่างเอาไว้เสมอ เราสามารถทำความเข้าใจมันได้ผ่านการวาดรูป ผ่านการสังเกต ผ่านเหตุและผล หรือผ่านการ breakdown ออกมาเป็นสมการย่อย ๆ เพียงแค่ในหลาย ๆ ครั้ง การเรียนการสอนในโรงเรียนไม่ได้ให้ความสำคัญกับการที่พาเราลงลึกไปสำรวจใต้ภูเขานำ้แข็งเท่านั้นเอง

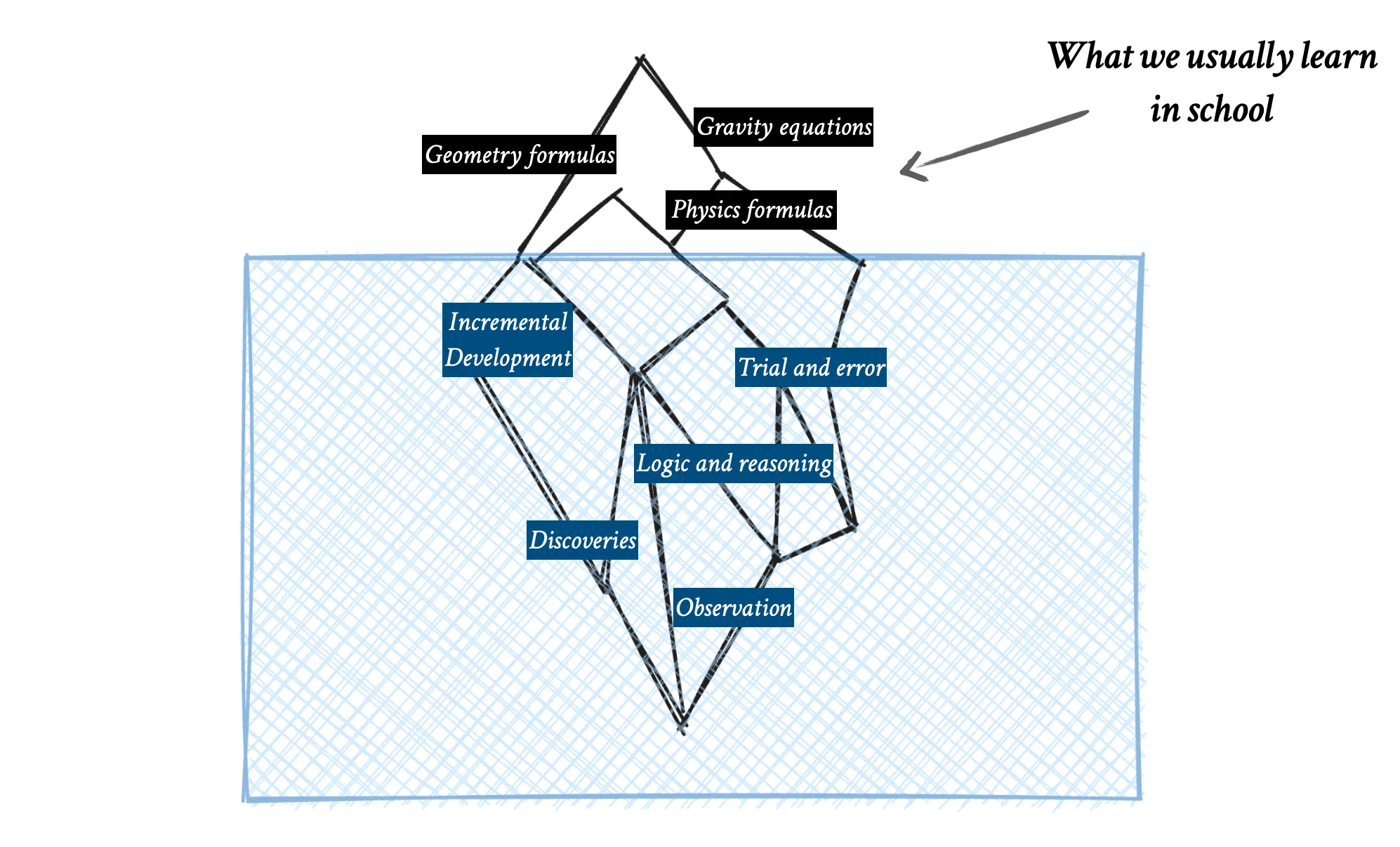
แน่นอนว่าการได้ลองทำความเข้าใจ ณ​ ตอนนั้น มันเปลี่ยนมุมมองต่อวิชาคณิตและมุมมองในการเรียนของตัวเราเองไปพอสมควร ถึงแม้ว่าตอนนั้นจะไม่ได้มานั่งตกผลึกออกมาต่อก็เถอะ

แล้วสรุปคณิตศาสตร์คืออะไร?

คณิตศาสตร์ as a ภาษา

เรามาเริ่มต้นจากคณิตศาสตร์ที่เราคุ้นเคยกันก่อนดีกว่า โดยปกติเวลาเราเรียนคณิตเราก็มักจะนึกถึงตัวเลข การคำนวณ การแก้โจทย์เพื่อหาค่าตัวแปรอะไรอย่างงั้นใช่ไหมครับ

สมมุติเรามีโจทย์ \(20 + 5 * 2\) เราก็สามารถคำนวณออกมาเป็น step ได้ เช่นเอา \(5 * 2 = 10\) จากนั้นเอา \(20 + 10\) ได้คำตอบออกมาเป็น 30

สิ่งที่เราพูดถึงอยู่นี้ถ้าจะเรียกว่าคณิตศาสตร์ก็คงจะไม่ถูกนัก ควรจะเรียกกว่า ‘การคำนวณ’ หรือ ‘Computation’ จะถูกกว่า

“Computation is an act of solving a problem by performing operations.”

ถามว่าเรารู้ได้ยังไงว่าเราต้องเอา 5 ไปคูณ 2 แล้วไปบวก 20? แล้วเรารู้ได้ยังไงว่า \(5 * 2 = 10\)?

เพราะเราเคยเรียนกันตอนประถมใช่ไหมหละครับว่าการบวกต้องทำยังไง และการคูณต้องทำยังไง แล้วลำดับความสำคัญในแต่ละ operation เป็นยังไง ต้องทำอะไรก่อนหลัง

จริง ๆ สิ่งนี้ก็คือสิ่งที่เรียกว่า ‘Algorithm’ หรือ “a finite, step-by-step instructions to solve problem.” นั่นเองครับ

ถ้าพูดให้เห็นภาพก็คือเราใช้ algorithm ที่เราถูกสอนตอนเด็ก (ว่าจะถ้าเจอวงเล็บจะต้องทำในวงเล็บก่อน ต้องทำคูณก่อนบวก ขั้นตอนในคูณเป็นยังไง และอื่น ๆ) มาทำ computation เพื่อให้ได้มาซึ่งคำตอบนั่นเอง

ซึ่งประเด็นอยู่ตรงนี้หละครับ ตรงที่ว่าเรามักสัปสนคำว่า computation กับคำว่า mathematics; เวลาเราเรียนวิชาคณิตศาสตร์ใน รร เราก็จะพบว่าหลาย ๆ ครั้งโจทย์จะให้คำนวณเพื่อหาค่าอะไรบางอย่างออกมาซึ่งนั่นมันคือ computation มันคือการ follow algorithm (ในขณะที่ skills ที่สำคัญกว่ามันคือการ “come up with algorithm” หรือ problem solving )

…

ถ้าพูดถึงคำว่า computation อีกคำนึงที่หลายคนน่าจะรู้จักคือคำว่า ‘Computer’

จริง ๆ computer ก็ไม่ได้ต่างกับคำว่า writer, dancer, driver หรอกครับ คำว่า computer มันก็คือ “a thing that does computation” นั่นหละ

“โรงเรียนกำลังสอนให้คนเป็น Computer ในขณะที่นักพัฒนาเก่ง ๆ ทั่วโลกกำลังสอน Computer ให้กลายเป็นคน (AI)” - อาจารย์ Dave Rawitat

งั้นถ้าสิ่งที่เรารู้จักกันคือ computation แล้ว math คืออะไร? เราลองมาเริ่มจากเหตุการณ์ง่าย ๆ กันก่อนดีกว่าครับ สมมุติว่าเรามี sequence อยู่ประมาณนี้

ถ้าเราลองดูแค่ 1, 3 เราอาจจะงงว่ามันคือ sequence ของอะไร แต่คราวนี้ถ้าเราลองสังเกตไปเรื่อย ๆ เราจะพบว่าตัวเลขมันเพิ่มขึ้นทีละสอง 1, 1 + 2, 1 + 2 + 2, 1 + 2 + 2 + 2, … เราจะพบว่ามันมี pattern ของมันอยู่ และด้วย pattern ตรงนี้เราสามารถเขียนอธิบายมันออกมาได้เป็น

หมายความว่า A ตัวที่ n เท่ากับ A ตัวก่อนหน้าบวกด้วย 2;

จากสมการด้านบนนี้นอกจากจะสั้นกระชับแล้ว ยังมีความชัดเจนในการอธิบาย pattern ที่เราจะสื่อสารอีกด้วย และแน่นอนว่ายิ่ง pattern มีความซับซ้อนมากเท่าไหร่ การจะอธิบายก็จะยิ่งยาก ดังนั้นภาษาที่มีความชัดเจน ไม่กำกวม ทุกคนอ่านแล้วเห็นภาพเดียวกันเลยมีความสำคัญมาก และภาษานั้นก็คือคณิตศาสตร์

(ลองคิดภาพว่าถ้าเราอธิบายโดยใช้ภาษาพูดมันจะยาวและมีความกำกวมมากแค่ไหน)

“Mathematics is a language that describes patterns, structure, and reasoning.”

Mathematics มันคือภาษาที่เราใช้อธิบาย pattern และ reasoning ของสิ่งต่าง ๆ ถ้าหากเราสังเกตการตกหรือการโยนของสิ่งของในอากาศหลาย ๆ ชิ้น เราอาจจะเห็น pattern บางอย่างซึ่งใช้ภาษาของคณิตศาสตร์อธิบายมันออกมาได้ เช่น ไม่ว่าจะโยนของขึ้นไปเร็วเท่าไหร่ ความเร็วจะค่อย ๆ ลดลง และความเร็วเป็น 0 จากนั้นก็ค่อยตกลงมา

หรือถ้าเราสังเกตทรงกลมหลาย ๆ ขนาดเราอาจจะเห็น pattern บางอย่างที่ใช้ math เขียนอธิบายออกมาได้

คณิตศาสตร์ as a เครื่องมือในการแก้ปัญหา

เมื่อเรามีภาษาแล้วย่อมต้องมีความหมาย และความหมายก็เป็นอะไรที่สามารถที่จะนำไปตีความต่อได้ เกิดเป็นการศึกษาในด้านต่าง ๆ (เช่น properties หรือ implication) จนเกิดเป็น theory และ application มากมาย ยกตัวอย่างเช่น

Arithmetic, Number Theory - คือการศึกษาเกี่ยวกับ Pattern ของการนับและตัวเลข

Geometry - ศึกษาเกี่ยวกับ Pattern ของรูปร่าง

Calculus - ศึกษาเกี่ยวกับ Pattern ของการเคลื่อนไหว หรือการเปลี่ยนแปลง

Logic - ศึกษาเกี่ยวกับ Pattern ของการให้เหตุผล

การศึกษาและการตีความหมายพวกนี้มันนำมาสู่ mathematical problem มากมายที่มีการ discuss มีการคิดต่อยอดกันมาเป็นพัน ๆ ปี มันนำมาสู่ algorithm ที่หลากหลาย, proof methods แบบต่าง ๆ หรือการพัฒนา notation ที่โตและหลากหลายมากขึ้น เช่นเดียวกับภาษาที่มีการ develop สร้างศัพท์ใหม่ ๆ อยู่ตลอดเวลา

ด้วยอะไรพวกนี้เราอาจพูดได้เหมือนกันว่า Mathematics มันเป็นเหมือนกับแหล่งของเครื่องมือชั้นดี ชุดความคิด วิธีการต่าง ๆ ที่เราสามารถหยิบมาใช้แก้ปัญหาต่าง ๆ ในชีวิตได้ เช่นเราเจอปัญหา ๆ นึง เราอาจจะหยิบ math model มาใช้ describe ปัญหาให้อยู่ในโลกของ math ได้ จากนั้นเราก็เลือกหยิบ algorithm ที่มีคนคิดมาให้แล้ว มา apply มา perform computation เพื่อแก้ปัญหาได้โดยตรง

เราคิดว่าคณิตศาสตร์มันสามารถมองได้ทั้งสองมุมเลย ทั้งในด้านของภาษา และในด้านของเครื่องมือในการแก้ปัญหา และถึงตอนนี้เราก็เชื่อว่าหลายคนน่าจะเห็นภาพคำว่าคณิตศาสตร์มากขึ้นแล้ว

เราควรจะเรียนคณิตศาสตร์กันยังไง ?

เพื่อให้เห็นภาพ ส่วนตัวอยากจะเปรียบเทียบกับ programming หรือการเขียนโปรแกรมสักนิดนึง เพราะคิดว่ามันมีความเหมือนกันอยู่พอสมควร

“Programming uses code as a language to describe algorithms.”

“Mathematic uses mathematical notation as a language to describe patterns, structure, and reasoning.”

Programming คือการเขียนโค้ด แต่เราจะเขียนโค้ดออกมาไม่ได้เลยถ้าหากว่าเราไม่สามารถที่จะคิด algorithm มาเพื่อแก้ปัญหาอะไรสักอย่างได้ หรือขาด problem-solving skills; หรือเราอาจจะเขียนโค้ดออกมาอ่านไม่รู้เรื่องเลย ถ้าเราไม่มีคำศัพท์และวิธีการเล่าเรื่องในหัวเยอะพอ (การ simplify algorithm, การเลือกใช้ data structures/algorithm ที่มีอยู่, หรือการเข้าใจ design principles)

เราคิดว่า Math ก็เหมือนกัน เราจะอธิบายสิ่งต่าง ๆ ออกมาไม่ได้เลยถ้าหากว่าเราไม่เห็นภาพของสิ่ง ๆ นั้นก่อน หรือเราขาด observation, pattern finding and reasoning skills; และเราคงจะ express ภาษาของคณิตศาสตร์ออกมาให้ดีไม่ได้เลย ถ้าเราไม่มีคำศัพท์และวิธีการเล่าเรื่องในหัวเยอะพอ (การ simplify formula, การหยิบเอา mathematical model ต่าง ๆ มาใช้อธิบายภาพ)

สุดท้ายถ้าถามว่าเราควรจะเรียนคณิตศาสตร์อย่างไร ในความเห็นส่วนตัวของเราเอง เราคงจะ “เรียนคณิตศาสตร์เหมือนที่เราเรียนภาษา”

เรียนคำศัพท์ใหม่ ๆ ฝึกสื่อสารเพื่ออธิบายภาพที่เราต้องการจะสื่อออกมา และเรียนรู้ว่าคนอื่นสื่อสารยังไงเพื่อปรับวิธีการเล่าเรื่อง สำนวนของตัวเอง เชื่อว่าเราจะค่อย ๆ ใช้ภาษาที่เรียกว่าคณิตศาสตร์นี้คล่องขึ้นแน่นอน