Big O Notation คืออะไร?

Computational Complexity

ปัญหาใดปัญหาหนึ่งมักจะมีวิธีการแก้ไขหรือ ‘Solution’ ได้หลากหลายทางเสมอ แต่คำถามนึงที่สำคัญก็คือ “เราจะเลือกวิธีการไหนมาใช้แก้ปัญหา ?” หรือบางคนอาจจะถามว่า “วิธีการไหนคือวิธีการที่ดีที่สุด ?”

แน่นอนว่าเราไม่สามารถตอบได้หรอกว่าวิธีการไหนคือวิธีการที่ดีที่สุด เว้นเสียแต่ว่าเรา define คำว่าดีและไม่ดีเสียก่อน ส่วนตัวเรามองว่ามันคือการตีกรอบของปัญหา มันคือการ list ออกมาว่าเรามีข้อจำกัดอะไรบ้าง 1,2,3,4 ซึ่งถ้าเราคิดวิธีแก้ปัญหาที่ตอบโจทย์กับกรอบนั้นได้ก็ถือว่าดี

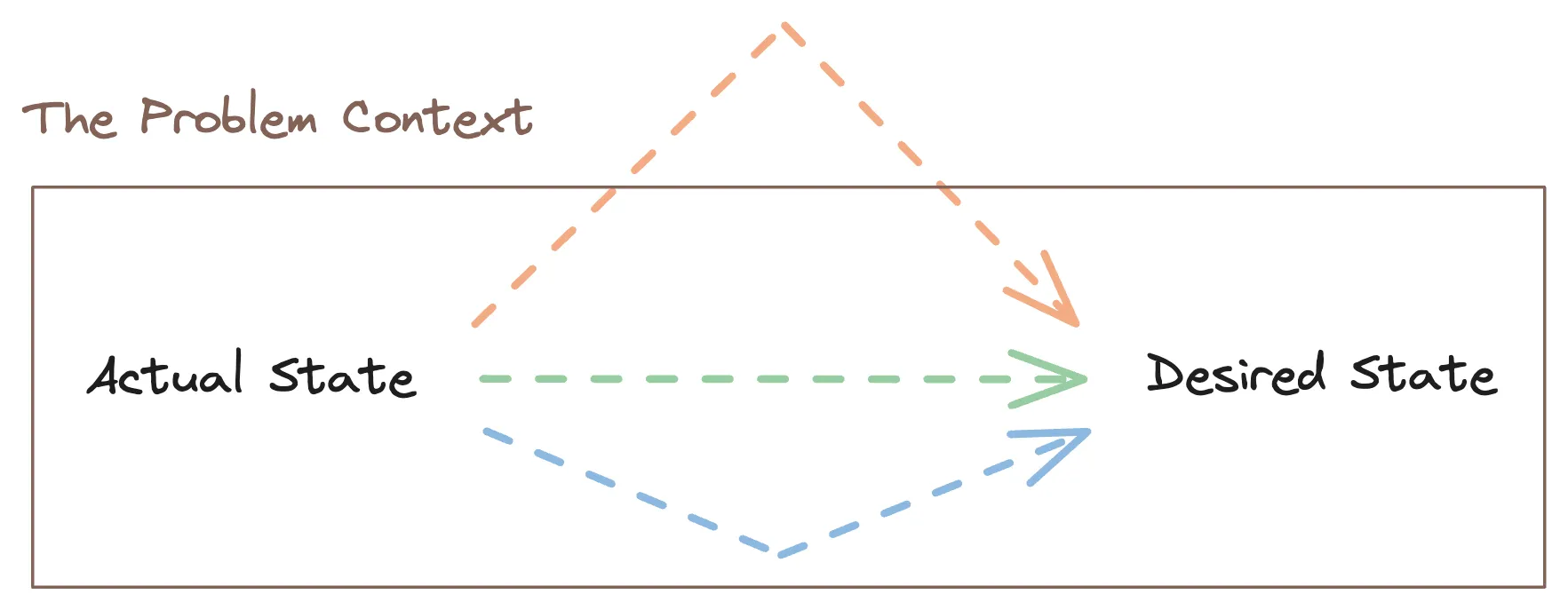
โดยเราจะเรียกกรอบที่เราตีขึ้นมานี้ว่า ‘บริบท’ หรือ ‘Context’ ของปัญหา ครับ

“ปัญหา” คืออะไร? มีโครงสร้างเป็นยังไง? และทำไมการเข้าใจคำ ๆ นี้ถึงสำคัญ

ปัญหาเป็นอะไรที่อยู่รอบตัวในชีวิตประจำวันของเราทุกคน แต่สิ่งที่เรามักเรียกมันจนเคยชินว่า “ปัญหา” จริง ๆ แล้วมันคืออะไร?

สามารถอ่านต่อเรื่องของ ‘ปัญหา’ แบบละเอียด ๆ ที่บทความด้านบนนี้ได้เลยครับ

การตีกรอบนี้เป็นอะไรที่สำคัญมาก ๆ เพราะมันส่งผลโดยตรงต่อการ design และการเลือกใช้วิธีแก้ปัญหา

ยกตัวอย่างเช่น ถ้าหากเราอยากจะทำเว็บไซต์ที่โชว์ข้อมูลอะไรบางอย่าง (เช่น jobs directory) ในตอนเริ่มต้นเว็บเราไม่ได้มีอะไรอัพเดตบ่อยขนาดนั้น และ budget ก็ไม่ได้เยอะ ดังนั้นเราอาจจะทำเว็บเป็น static site และในส่วนของข้อมูลอาจจะใช้ Google sheets, Airtable หรืออาจจะเก็บลง JSON file แล้วดึงมาใช้งานตรง ๆ เลยก็ได้

แต่พอเว็บเริ่มโตขึ้น ผู้ใช้งานต้องการข้อมูลที่ real-time และ up to date มากขึ้น ตอนนั้นบริบทก็อาจจะเปลี่ยนไป ทำให้วิธีการเดิมอาจจะไม่เหมาะกับปัญหาที่เราแก้อยู่

How Levels.fyi scaled to millions of users with Google Sheets as a backend

จะเห็นว่ามีปัจจัยหลายอย่างที่ส่งผลต่อการตัดสินใจเลือกวิธีแก้ปัญหา ๆ นึง ยกตัวอย่างเช่นถ้าหากว่าเราจะทำเว็บซักเว็บนึง เราอาจจะต้องคำนึงถึง

งบประมาณที่เรามี
เวลาหรือ timeline
จำนวนนักพัฒนา
ความเชี่ยวชาญหรือ skills ของแต่ละคนในทีม
จำนวนคนใช้งานที่จะเข้ามาใช้งานในเว็บของเรา
Goal หรือ objective ของสิ่งที่เรากำลัง focus อยู่ และอื่น ๆ

ซึ่งกรอบหรือสิ่งที่เราต้องคำนึงก็จะเปลี่ยนไปตามปัญหาที่เปลี่ยนไปด้วย เช่นถ้าเป็นการจัดงานกิจกรรม เราอาจจะต้องคำนึงเรื่อง space (พื้นที่จัดงาน), ระยะเวลา, กิจกรรมก่อนหน้าและหลังจากนั้น หรือถ้าหากเป็นการออกแบบเก้าอี้ขึ้นมาสักตัว เราอาจจะต้องคำนึงถึงความทนทาน รูปแบบการใช้งาน และอื่น ๆ เป็นต้น

ในแง่ของการออกแบบ computational algorithm ก็เช่นกันครับ เราจำเป็นต้องคำนึงถึงข้อจำกัดต่าง ๆ ไม่ว่าจะเป็นระยะเวลาในรัน (Time) หรือพื้นที่ที่ใช้เก็บข้อมูลในการรัน (Space) เราเรียก cost หรือ resources ที่ต้องใช้ในการรัน algorithm นึง ๆ นี้ว่า ‘Computational Complexity’

เพิ่มเติม: Algorithm ที่ทำงานได้ไวไม่ใช่คำตอบเสมอไป เช่นบางครั้งการออกแบบ algorithm อาจแลกมาด้วยพื้นที่เก็บข้อมูลเพิ่มขึ้น (Time-memory tradeoffs) หรือ algorithm ที่ทำงานได้ไวอาจจะแลกมากับความซับซ้อนในการ implement ที่เพิ่มขึ้น เป็นต้น

ซึ่งมันนำมาสู่คำถามที่สำคัญต่อมาก็คือ

“เราจะวัด ‘Computational Complexity’ หรือ resources ที่ใช้ในการรัน algorithm ของเรายังไง ?”

เพราะเราจะได้เอาสิ่งที่เราวัดได้ ไปเปรียบเทียบ (compare) กับ algorithm อื่น ๆ ไป optimize ให้มันใชั resource น้อยลง หรือไปประเมิน (evaluate) ได้ว่า algorithm นี้ตอบโจทย์ context หรือกรอบที่เราวางไว้หรือยัง

ซึ่งนี่ก็เป็นคำถามที่เราจะไป explore ใน chapter นี้กันครับ

โดยในบทนี้จะขอยกตัวอย่างหลักเป็นการวัด Time complexity นะครับ

1. นาฬิกาจับเวลา

หนึ่งในวิธีการที่ง่ายที่สุดและตรงไปตรงมาที่สุด ในการวัดระยะเวลาในการรัน algorithm ก็คือการ ‘ใช้นาฬิกาจับเวลา’

โดยเราก็อาจจะลองใส่ input ค่าหนึ่งเข้าไป (ซึ่งอาจจะเป็นค่าที่มากที่สุดที่เป็นไปได้เวลาเราจะเอาไปใช้งานจริง) จากนั้นก็ลองรันดู อาจจะหลาย ๆ ครั้งก็ได้และวัดค่าเฉลี่ยออกมา

เพื่อให้เห็นภาพ เราอยากจะขอยกตัวอย่างจาก challenge problem ใน chapter ที่แล้ว function add(n); ซึ่งในที่นี้อยากขอวัดเวลาของ solution แรกที่ใช้ for-loop เทียบกับอีก solution นึงที่ใช้สูตรทางคณิตศาสตร์ในการคำนวนตรง ๆ ออกมาเลย

เพิ่มเติม: สำหรับการจับเวลาแบบนี้เรามักเรียกมันว่าการวัด ‘Wall-clock time’ (หรือ ‘Elapsed real time’) ซึ่งเราสามารถใช้ function console.time() และ console.timeEnd() ในการวัดได้ โดยเราแค่เอา function สองตัวนี้ไปครอบระหว่างโค้ดที่เราอยากจะวัดเวลา อ่านเพิ่มเติม

ตาราง compare ระยะเวลาที่ได้จากการรัน function add ใน input size ขนาดต่าง ๆ

จากรูปจะเห็นว่าวิธีการ for-loop ถ้า input size มากขึ้นเรื่อย ๆ เวลาที่ใช้รันก็จะมากขึ้นเรื่อย ๆ เช่นกัน ส่วนวิธีการที่สอง ถึงแม้ว่า input size จะมากขึ้น แต่จะเห็นได้ว่าแทบไม่มีผลกระทบกับระยะเวลาในการรันเลย (เวลาในการรันเท่า ๆ กัน ไม่ว่า input size จะเล็กหรือใหญ่ก็ตาม)

จากข้อมูลนี้เองเราอาจจะสรุปได้ว่า algorithm 1 ช้ากว่า algorithm 2 จากการเอาเวลาของ input size ใหญ่ ๆ มาเทียบกัน และเวลาในการรัน algorithm 1 จะโตขึ้นตาม input size ในขณะที่ algorithm 2 มีระยะเวลาในการรันที่คงที่

แต่แน่นอนว่าการวัดด้วยวิธีการนี้มีข้อเสียหลายอย่าง ยกตัวอย่างเช่น

เวลาที่ไม่แน่นอนในการรันในแต่ละครั้ง: ถ้าเราลองสังเกต algorithm 2 ดูเราจะพบว่า add(100000000) รันช้ากว่า add(10000) ; ซึ่งข้อมูลที่มีความผันผวนนี้มันทำให้เราเอาไป compare, optimize, evaluate ต่อได้ยากมาก
เวลาที่วัดได้แตกต่างกันเมื่อเปลี่ยน hardware ที่ใช้รัน: 1 instruction ในแต่ละ hardware ใช้เวลาในการประมวลผลไม่เท่ากัน ดังนั้นถ้าเราอยากจะเปรียบเทียบหลาย ๆ algorithm ด้วยกัน เท่ากับว่าเราต้องรันและวัดเวลาของแต่ละ algorithm บน hardware เดียวกันใหม่ทั้งหมด
จำเป็นต้อง implement algorithm ให้เสร็จก่อน: เราจะรันและวัดผลไม่ได้ถ้าหากว่าเราไม่ implement algorithm นั้นให้เสร็จก่อน ซึ่งการ implement ก็เป็นอะไรที่มี cost ค่อนข้างสูง

ด้วยปัญหานี้เอง มันก็ทำให้เรากลับมาที่คำถามเก่าที่ว่า “มันมีวิธีการวัดที่ดีกว่านี้ไหม ?”

2. นับจำนวน Instruction

ในเมื่อ instruction เดียวกันในแต่ละ hardware ใช้ระยะเวลาในการรันที่ไม่เหมือนกัน แถมจับเวลาตรง ๆ ก็มีความผันผวนอีก ดังนั้นแทนที่เราจะวัดเวลาตรง ๆ เราก็วัดจากจำนวน instruction เลยสิว่า algorithm นี้มีจำนวน instruction เทียบกับ input size เป็นเท่าไหร่

ในที่นี้จะขอใช้คำว่า ‘Cost’ ละกันนะครับ โดย 1 instruction มีค่าเท่ากับหนึ่ง cost เช่นถ้าเรานับ algorithm นึงได้ 3 instruction ก็แสดงว่า algorithm นี้มี \(Cost = 3\)

เพื่อให้เห็นภาพมากขึ้นเรามาลองนับ cost ของ function add(n) แบบ for-loop กันครับ

1
function add(n) {
2
  let result = 0;
3
  for (let i = 1; i <= n; ++i) {
4
    result += i;
5
  }
6
  return result;
7
}

เราสามารถเริ่มนับจากบรรทัดที่ 2 (เพราะเป็นบรรทัดแรกที่ function เริ่มทำงาน) โดยบรรทัดที่ 2 มี instruction เดียวก็คือการ set ค่าตัวแปร ดังนั้นบรรทัดนี้มี \(Cost = 1\)

ต่อมาบรรทัดที่ 3 จะเห็นว่าโค้ดจะมีการทำงานเกิดขึ้นทั้งหมด 3 instructions ด้วยกัน โดยโค้ดจะทำงานตามลำดับดังนี้

let i = 1 เป็นการกำหนดค่าตัวแปรเริ่มต้น; \(Cost = 1\)
i <= n และ ++i; \(Cost = 2\)
For-loop นี้จะทำงานทั้งหมด n ครั้ง (loop i ตั้งแต่ 1 → n) ดังนั้นเราต้องทำ instruction ในข้อ (2) ทั้งหมด n ครั้ง; \(Cost = 2n\)

ดังนั้น cost ทั้งหมดในบรรดทัดที่ 3 ก็คือ \(1 + 2n\)

บรรทัดที่ 4 มีแค่ 1 instruction แต่ว่า instruction นี้มันอยู่ใน for-loop ที่รัน n ครั้ง นั่นหมายความว่าบรรทัดนี้ต้องทำงาน n ครั้งด้วย; \(Cost = n\)

ส่วนบรรทัดที่ 6 เป็นก็มี 1 instruction; \(Cost = 1\)

1
function add(n) {
2
  let result = 0; // Cost = 1
3
  for (let i = 1; i <= n; ++i) {
4
    // Cost = 2n + 1
5
    result += i; // Cost = 1 * n = n
6
  }
7
  return result; // Cost = 1
8
}

สุดท้ายนี้เราก็แค่รวม cost ของทุกบรรทัดทั้งหมดเข้าด้วยกัน เราก็จะได้ cost ทั้งหมดของ algorithm นี้ออกมาเป็น:

Cost(n) = 1 + 1 + 2n + n + 1 = 3n + 3

นั่นหมายความว่าถ้าเกิด n = หนึ่งล้าน เท่ากับว่าโค้ดเราจะทำงานประมาณ 3 ล้าน instruction เลยทีเดียว ซึ่งยิ่ง input size มีค่ามากขึ้นเท่าไหร่ instruction ก็จะโตตามไปด้วย (เราเรียกว่าใช้ Time complexity แบบ ‘Linear time’)

เพิ่มเติม: จำนวน cost ที่วัดได้เมื่อ n มีค่า ๆ หนึ่ง ไม่สำคัญเท่ากับอัตราการเติบโตของ cost (หรือที่เราเรียกกันว่า ‘Growth rate’) ถ้า \(Cost_A(n) = n\) และ \(Cost_B(n) = n^2\) ถ้าเราให้ n = 10 ซึ่ง CostA = 10, CostB = 100 เราไม่สามารถสรุปได้ว่า A เร็วกว่า B สิบเท่า เพราะถ้าเราให้ n = 100 เราจะพบว่า A เร็วกว่า B หนึ่งร้อยเท่า จะเห็นว่าจำนวนเท่าไม่ได้บอกอะไรเราเลย สิ่งที่เป็นประโยชน์กับเรามากกว่าคือ cost เติบโตเทียบกับ n เป็นเท่าไหร่

นี่ก็เป็นวิธีนึงในการวัด Time complexity ซึ่งจะเห็นว่ามันมีความ precise มากกว่าแบบแรกเยอะ เพราะไม่มีความผันผวนทางเวลาเข้ามาเกี่ยวข้อง เราสามารถเอาจำนวน instruction ไป compare กับ algorithm อื่น ๆ ได้ เราสามารถ optimize และวัดผลได้ชัดเจนขึ้น และเราสามารถ evaluate ได้ว่าถ้า input size เราใหญ่ประมาณนี้ เราจะใช้ instruction ประมาณเท่าไหร่ ซึ่งมันเกินกรอบ resources ที่เราตีเอาไว้ไหม

ที่สำคัญก็คือเราสามารถประเมินได้โดยที่ยังไม่ต้อง implement algorithm เลยด้วยซ้ำ

1
function add(n) {
2
  let a = n + 1;
3
  let b = n / 2;
4
  return a * b;
5
}

แน่นอนว่าวิธีการนี้มันก็ work ในแบบของมัน แต่ถ้าเราลองประเมิน algorithm ที่ซับซ้อนขึ้นไปเรื่อย ๆ เราก็จะบ่นกับตัวเองว่า “ทำไมชีวิตมันถึงต้องยากขนาดนี้ว่ะ ?” ขนาดแค่นับ instructions ของ for-loop เดียวยังเหนื่อยและเสียเวลาขนาดนี้ ไม่ต้องพูดถึง algorithm ที่มี nested-loop, conditional-loop, recursion เลย นับไม่ไหวแน่นอน

คำถามก็คือเราจำเป็นต้องรู้จำนวน instruction ที่เป็ะขนาดนั้นไหม ?

แน่นอนครับว่าถ้าเราไม่ได้ต้องการที่จะ optimize เพื่อลดจำนวน instruction แบบละเอียด ๆ หรือพัฒนา algorithm บนระบบที่ทรัพยากรมีจำกัดมาก ๆ หรืออะไรแบบนั้น คำตอบก็คือ ‘ไม่จำเป็น’ ครับ ยกตัวอย่างเช่น

ถ้าให้ Algorithm A มี \(Cost_A = 3\) กับ B มี \(Cost_B = 25\); แน่นอนว่าถ้าเอาไปรันจริง ๆ มันแทบจะไม่ต่างเลย ซึ่งเรารู้แค่ว่า algorithm A และ B มี cost เป็น constant ก็พอแล้ว (ไม่ขึ้นกับ input)

หรือถ้าให้ Algorithm A มี \(Cost_A(n) = 3n^4 + 3n + 25\) กับ B มี \(Cost_B(n) = 2n^4 + 200\) จริง ๆ เรารู้แค่ว่า \(Cost_A(n) \approx 3n^4\) และ \(Cost_B(n) \approx 2n^4\) ก็พอแล้ว เพราะว่าเมื่อ input size มีค่ามาก ๆ เราจะพบว่าตัวที่มันกิน resources หลักจริง ๆ ก็คือ term \(n^4\) ส่วน term ที่เหลืออย่าง \(3n + 25\) กับ \(200\) มันไม่ได้ significant อะไรเมื่อ \(n\) มีค่ามาก ๆ หรือเข้าใกล้ \(\infty\) (ดังนั้นเราเลือกที่จะตัดมันออกได้)

หรือถ้าไปอีกขั้นนึงเลยคือ estimate แค่ \(Cost_A(n) \approx n^4\) และ \(Cost_B(n) \approx n^4\) ไปเลย (ตัด constant ที่คูณด้านหน้าออก) เพราะมันก็เหมือนตัวอย่างแรกหละที่เราบอกว่า 3 กับ 25 มันก็ constant เหมือนกัน ดังนั้นสุดท้าย \(Cost_A(n) \approx 3n^4\) กับ \(Cost_B(n) \approx 2n^4\) มันก็คือ

Cost(n) = \text{some constant} * n^4

ยังไง A กับ B มันก็มี Time complexity ที่โตแบบ \(n^4\) เหมือนกันอยู่ดี

จะเห็นว่าสุดท้ายแล้ว มันไม่มีอะไรผิดหรือถูกหรอก เราจะวัด Time complexity ออกมาเป็นจำนวน instructions แบบเป็ะ ๆ หรือเราจะ estimate จนเแบบคร่าว ๆ จนเหลือแค่ term ที่ significant ที่สุดก็ได้ สุดท้ายมันขึ้นอยู่กับคำถามที่ว่า

“คำถามที่เรากำลังหาคำตอบ หรือเป้าหมายที่เรากำลังทำอยู่ มันต้องการ Information ที่ละเอียดมากน้อยแค่ไหน ?”

ถ้าต้องการความละเอียดมากก็อาจจะต้องใช้ effort ในการวัดเยอะหน่อย แต่ถ้าเราแค่อยากรู้ว่า A กับ B มันต่างกับแบบ significant ไหมมาก ๆ เราก็อาจจะลดความละเอียดลง แลกกับที่เราจะได้ไม่เสียต้อง effort กับการวัดที่มากเกินความจำเป็น

3. Asymptotic Analysis

เราเรียกการ estimate cost แบบคร่าว ๆ เมื่อ input size มีค่ามาก ๆ หรือเข้าใกล้ infinity เหมือนที่เราพึ่งจะทำกันไปว่า การทำ ‘Asymptotic Analysis’

asymptote (n.) “straight line continually approaching but never meeting a curve,” 1650s, from Greek asymptotos “not falling together,”

Asymptote คือเส้นหรือ ‘line’ ที่เข้าใกล้ curve หนึ่ง ๆ มากขึ้นเรื่อย ๆ แต่ไม่มีวันบรรจบกับ curve นั้น ยกตัวอย่างเช่น \(f(x) = 1/x\)

สีฟ้า = Curve, สีชมพู = Asymptote line (ลองเลื่อนปุ่มสีเขียวเพื่อดูค่า y)

เราสามารถพูดได้ว่าเมื่อ x มีค่ามากขึ้นเรื่อย ๆ ค่า y หรือ \(f(x)\) ก็เข้าใกล้ 0 มากขึ้นเรื่อย ๆ; ในทางตรงกันข้าม เมื่อค่า x เป็นค่าลบและน้อยลงเรื่อย ๆ ค่า y ก็จะวิ่งเข้าใกล้ 0 มากขึ้นเรื่อย ๆ เช่นกัน

เราเรียกสิ่งนี้ว่า ‘limit’ มันคือค่าบางอย่าง (value) ที่เราเข้าใกล้มันขึ้นเรื่อย ๆ เมื่อ x เข้าใกล้หรือวิ่งเข้าสู่ค่าบางค่า เช่น ยิ่งเรามีจำนวน deadline ในชีวิตเข้าใกล้ 10 เท่าไหร่ ความสุขของเรา (happiness) ก็ยิ่งลดลงหรือเข้าใกล้ 0 มากขึ้นไปเรื่อย ๆ

เราอาจจะพูดได้ว่า limit ของ happiness เมื่อ deadline เข้าใกล้ 10 ก็คือ 0

\lim_{deadline \to 10} hapiness(deadline) = 0

หรือในตัวอย่างนี้ limit ของ \(f(x)\) เมื่อ x วิ่งเข้าสู่ \(\infty\) ก็คือ 0

\lim_{x \to \infty} f(x) = 0 \text{\ \ and \ } \lim_{x \to -\infty} f(x) = 0

(ส่วนเส้น \(y = 0\) ก็คือเส้นที่เราเรียกมันว่า ‘Asymptote’ นั่นเอง)

Asymptotic analysis จริง ๆ แล้วมันก็คือวิธีที่ใช้อธิบาย limit behavior ของ function หนึ่ง ๆ เมื่อ argument วิ่งเข้าสู่ infinity นั้นหละ; หรือถ้าพูดให้ง่ายขึ้น มันคือคำถามที่ว่า

“เมื่อ argument มีค่ามาก ๆ หรือวิ่งเข้าสู่ infinity; function ดังกล่าวมัน ‘ทำตัว’ ยังไง ?”

ยกตัวอย่างเช่นในตอนท้ายของ section ที่แล้ว (ที่เรา estimate cost กัน) เราสามารถพูดได้ว่า \(Cost_A(n) = 3n^4 + 3n + 25\) ‘ทำตัวเหมือน’ \(f(n) = n^4\) เมื่อ n เข้าใกล้ \(\infty\) (เพราะเมื่อ n มีค่ามาก ๆ terms ที่เหลือมันไม่ significant อะไร เลยตัดออกได้)

หรือเราอาจจะพูดออกมาว่า

“\(Cost_A(n)\) is asymptotic to \(n^4\)”

ซึ่งเรามี ‘Asymptotic Notation’ หลายตัวเลยที่เราสามารถใช้ในการสื่อสารสิ่งที่เราอยากจะสื่อเหมือนประโยคข้างต้นนี้ ไม่ว่าจะเป็น Big Theta, Big Omega, Little Omega, Little O รวมไปถึง Big O Notation ที่หลาย ๆ คนรู้จักหรือเคยได้ยินด้วยนั่นเอง

Big-O Notation

Mathematical notation ก็เป็นเหมือนกับ ‘คำ’ ในภาษา ๆ หนึ่ง และคำใด ๆ ก็ตามย่อมมีความหมายที่เก็บอยู่ด้านหลังของคำ ๆ นั้น ที่เมื่อเราเข้าใจมันแล้ว เราก็จะสามารถหยิบมันมาใช้ในการสื่อสารหรือ express อะไรบางอย่างที่เราต้องการได้

ดังนั้นเพื่อที่จะเข้าใจสิ่งที่เรียกว่า ‘Big O Notation’ เรามาเริ่มจากการทำความเข้าใจนิยาม (definition) ของมันกันครับ

\(f(n)\) is a big O of \(g(n)\); If there exists an \(n_0\) and a constant \(c > 0\) such that for all \(n > n_0\), \(|f(n)| ≤ c * g(n)\)

ซึ่งเราสามารถเขียน “\(f(n)\) is a big O of \(g(n)\)” ได้ว่า

f(n) = O(g(n)) \text{\ \ \ as \ } n \rightarrow \infty

โอเค.. มันอาจจะฟังดูน่ากลัวหรือเป็นอะไรที่ดูเข้าใจยาก แต่จริง ๆ แล้วมันไม่ได้ยากขนาดนั้น เดี๋ยวเรามาลอง breakdown และทำความเข้าใจไปด้วยกันดีกว่า

\(f(n) = O(g(n))\) ก็ต่อเมื่อ เราสามารถหาค่าสองค่าได้ ก็คือ \(n_0\) และค่า \(c\) ที่ทำให้ condition บางอย่างเป็นจริง โดยที่ \(c\) เป็นจำนวนจริงบวก (\(c > 0\)) และค่า \(n_0\) คือค่าที่กำกับว่าค่า \(n\) หรือ argument ของ function จะต้องมากกว่าค่านี้ (\(n > n_0\))

โดยที่ condition นั้นก็คือ \(|f(n)| ≤ c*g(n)\) ซึ่งถ้าเรามองเป็นภาพเราก็จะพอเห็นว่าจะมี function สองเส้น โดยที่ \(|f(n)|\) จะอยู่ด้านล่าง ในขณะที่ \(c*g(n)\) อยู่ด้านบนเมื่อ (\(n > n_0\))

ยกตัวอย่างเช่น ถ้าหากเราอยากจะหา Big O ของ \(f(n) = 2n^2 + 3n\) เราก็แค่ต้องหา \(g(n)\), \(c\) และ \(n_0\) ที่ทำให้ \(c*g(n)\) มีค่ามากกว่า \(|f(n)|\) เมื่อ \(n > n_0\)

ซึ่งถ้าหากว่าเราสามารถหาตัวอย่าง (แค่ตัวเดียว) ที่ตอบกับ condition ข้างต้นได้เราก็สามารถที่จะเขียน Big O ของ \(f(x)\) ออกมาได้

ยกตัวอย่างเช่น เราอาจจะลองยกตัวอย่างเลขเยอะ ๆ หน่อยที่ทำให้ condition นั้นเป็นจริง \(g(n) = n^2\), \(c = 10\), \(n_0 = 100\) เราก็จะสรุปออกมาได้ว่า \(f(x) = O(g(n)) = O(n^2)\)

นี่เองเป็นเหตุผลว่าทำไมหลายคนเรียก Big O ว่าเป็น ‘Upper Bound’ หรือ ‘Worst Case’ เพราะ \(c*g(n)\) เป็นเหมือนกับเส้นด้านบนที่ \(f(x)\) ไม่มีทางจะมากหรือเลยไปกว่าเส้นนี้ได้แล้วนั่นเอง

Asymptotic Notation อื่น ๆ

อย่างที่เกริ่นเอาไว้ว่า asymptotic notation ไม่ได้มีแค่ Big O แค่ตัวเดียวแต่ยังมีตัวอื่น ๆ อีก และแต่ละตัวก็มี definition ที่แตกต่างกันไป

ใน section นี้เลยอยากจะมาแนะนำ notation ที่คิดว่าสำคัญและสามารถเอาไปใช้ได้เพิ่มอีก 2 ตัว นั่นก็คือ ‘Big Omega’ และ ‘Big Theta’

Big-Omega Notation

\(f(n) = \Omega(g(n))\); If there exists an \(n_0\) and a constant \(c > 0\) such that for all \(n > n_0\), \(c*g(n) ≤ |f(n)|\)

ความแตกต่างกับ Big O ก็คือ condition ที่แตกต่างกันที่ โดยที่ \(c*g(n)\) จะน้อยกว่า \(|f(n)|\) ซึ่งถ้าหากว่าเราลองเอา function ไป plot เป็นกราฟดูเราก็จะเห็นภาพแบบนี้ ⤵

จากภาพจะเห็นว่า เราสามารถใช้ Big Omega ในการอธิบาย ‘Lower Bound’ หรือ ‘Best Case’ ได้

Big-Theta Notation

\(f(n) = \Theta(g(n))\); If there exists an \(n_0\) and a constant \(c_1, c_2 > 0\) such that for all \(n > n_0\), \(c_1*g(n) ≤ |f(n)| ≤ c_2*g(n)\)

ถ้าหากว่าเราสังเกตที่ condition เราก็จะพบว่ามันคือ Big O รวมกับ Big Omega นั้นหละ ซึ่งถ้าหากว่าเราลองมองเป็นภาพก็จะเป็นแบบนี้

จากกราฟจะเห็นว่า เส้นขอบบนและขอบล่างมันคือ \(g(n)\) เหมือนกัน ซึ่งก็หมายความว่า Big O กับ Big Omega จะมีค่าเท่ากัน ดังนั้นเราก็สามารถใช้ Big Theta ในการเขียนอธิบายออกมาได้เลย เช่น \(f(x) = O(n^2) = \Omega(n^2)\) เราก็สามารถเขียนได้ว่า \(f(x) = \Theta(n^2)\)

เราสามารถใช้ Big Theta ในการอธิบาย ‘Tight Bound’ หรือกรณีที่ ‘Best Case’ และ ‘Worst Case’ ของ algorithm ของเราใช้ complexity เท่ากัน

1
function run(n) {
2
  let result = 0;
3
  for (let i = 1; i <= n; ++i) {
4
    for (let j = 1; j <= i; ++j) {
5
      result += j;
6
    }
7
  }
8
  for (let i = 0; i < n / 2; ++i) {
9
    result += 1;
10
  }
11
  return result;
12
}

สุดท้ายแล้วจะเห็นว่า notation แต่ละตัวก็มี definition ที่แตกต่างกันที่เราสามารถหยิบมาใช้สื่อในสิ่งที่เราอยากสื่อได้ไม่ว่าจะเป็น upper bound (worst case), lower bound (best case) หรือ tight bound

มันทำให้เราสื่อสารได้ดีขึ้น ตรงไปตรงมามากขึ้น และกำกวมน้อยลง

Exercises

ถ้าหากว่าเราเล่นเกมทายเลข โดยนาย A คิดเลขขึ้นมาในใจหนึ่งเลข (นาย A ตอบได้แค่ มากกว่า, น้อยกว่า, และถูกต้อง) และนาย B เป็นคนทาย ถ้าหากว่าเลขที่ต้องทายอยู่ในช่วง 1 ถึง 10 ล้าน อย่างแย่ที่สุดนาย B ต้องทายทั้งหมดกี่รอบ ? และ Big O ของการทายของนาย B คือเท่าไหร่ ?
Asymptotic notation อื่น ๆ นอกจาก Big O มีอะไรบ้าง ? และเราใช้มันในสถานการณ์ไหน ?
เมื่อไหร่ที่เราควรวัด cost แบบละเอียดและเมื่อไหร่ที่เราควร estimate cost แบบคร่าว ๆ ?
เรียงลำดับ \(O(\sqrt n)\), \(O(n)\) และ \(O(log_2 n)\) จากช้าที่สุดไปเร็วที่สุด
ลองยกตัวอย่าง algorithm ที่มี Big O เป็น \(O(nlogn)\) และ \(O(n!)\)

Challenge Problem

เขียน function ที่ชื่อว่า findDuplicateNumber โดยที่ function นี้จะรับ array ของตัวเลขเข้ามา (arr.length ≥ 1) โดยมีโอกาสที่ตัวเลขตัวใดตัวหนึ่ง (แค่ 1 ตัวเท่านั้นหรืออาจจะไม่มีเลยก็ได้) ใน array จะปรากฏขึ้นมากกว่า 1 ตัว

Return ค่าออกมาเป็นตัวเลขที่ซ้ำกัน หรือถ้าหากว่าไม่มีตัวซ้ำเลยให้ return -1

พยายามคิด solution หลาย ๆ แบบและอย่าลืมคำนวน Time/Space Complexity (Big O) ในแต่ละ solution ก่อน implement นะครับ

Example 1:

Input: [1,2,3,3,4]

Output: 3

Example 2:

Input: [1,2,3,4]

Output: -1

Explaination: ไม่มีค่าที่ซ้ำกันเลยดังนั้น return -1

Solution #1

เราสามารถ loop i ไปทีละตัวตั้งแต่ 0 → arr.length - 1; จากนั้น loop j ตั้งแต่ i + 1 → arr.length - 1 และเช็คว่ามี arr[i] === arr[j] ไหม ถ้าหากว่ามีก็แสดงว่ามีค่าที่ซ้ำเกิดขึ้น

1
function findDuplicateNumber(arr) {
2
  for (let i = 0; i < arr.length; ++i) {
3
    for (let j = i + 1; j < arr.length; ++j) {
4
      if (arr[i] === arr[j]) return arr[i];
5
    }
6
  }
7

8
  return -1;
9
}

Time Complexity: \(O(n^2)\), Space Complexity: \(O(1)\)

Solution #2

อีกวิธีการนึงคือเราสามารถ sort array จากนั้นเช็คว่ามีค่า arr[i] === arr[i+1] ไหม (เพราะเมื่อ sort แล้ว ถ้าหากว่ามีเลขที่ซ้ำมันก็จะอยู่ติดกันเพราะมี value เท่ากัน)

1
function findDuplicateNumber(arr) {
2
  arr.sort();
3
  for (let i = 0; i < arr.length - 1; ++i) {
4
    if (arr[i] === arr[i + 1]) return arr[i];
5
  }
6
  return -1;
7
}

Time Complexity: \(O(nlogn)\), Space Complexity: \(O(1)\)

การ Sort array (ใน JS และอีกหลาย ๆ ภาษา) มี Time Complexity เป็น \(O(nlogn)\) ดังนั้น Time Complexity ในข้อนี้จะมีค่าเป็น: \(O(nlogn) + O(n) = O(nlogn)\)

Solution #3

อีกหนึ่งวิธีที่ทำได้คือจำค่าเอาไว้ก่อนและถ้าหากว่าเราไปเจอเลขที่ซ้ำกับเลขที่เราเคยจำไว้ เราก็แค่ return ค่าที่ซ้ำนั้นออกมา ซึ่งเราสามารถใช้ data structure ที่ชื่อว่า map ในการจำค่าได้ โดยที่ให้ key เป็นตัวเลข ส่วน value เป็น boolean (true ถ้าหากว่าเคยเจอเลขนี้แล้ว)

1
function findDuplicateNumber(arr) {
2
  const map = new Map();
3
  for (let i = 0; i < arr.length; ++i) {
4
    if (map.has(arr[i])) return arr[i];
5
    map.set(arr[i], true);
6
  }
7

8
  return -1;
9
}

Time Complexity: \(O(n)\), Space Complexity: \(O(n)\) (เพราะมีการเก็บค่าลงใน map ตาม input size n = arr.length)